VIX指数

VIX指数（英: VIX Index）またはCBOEボラティリティ指数（英: CBOE Volatility Index）とは、シカゴ・オプション取引所（CBOE）が、S&P 500を対象とするオプション取引の満期30日のインプライド・ボラティリティを元に算出し、1993年より公表しているボラティリティ指数。

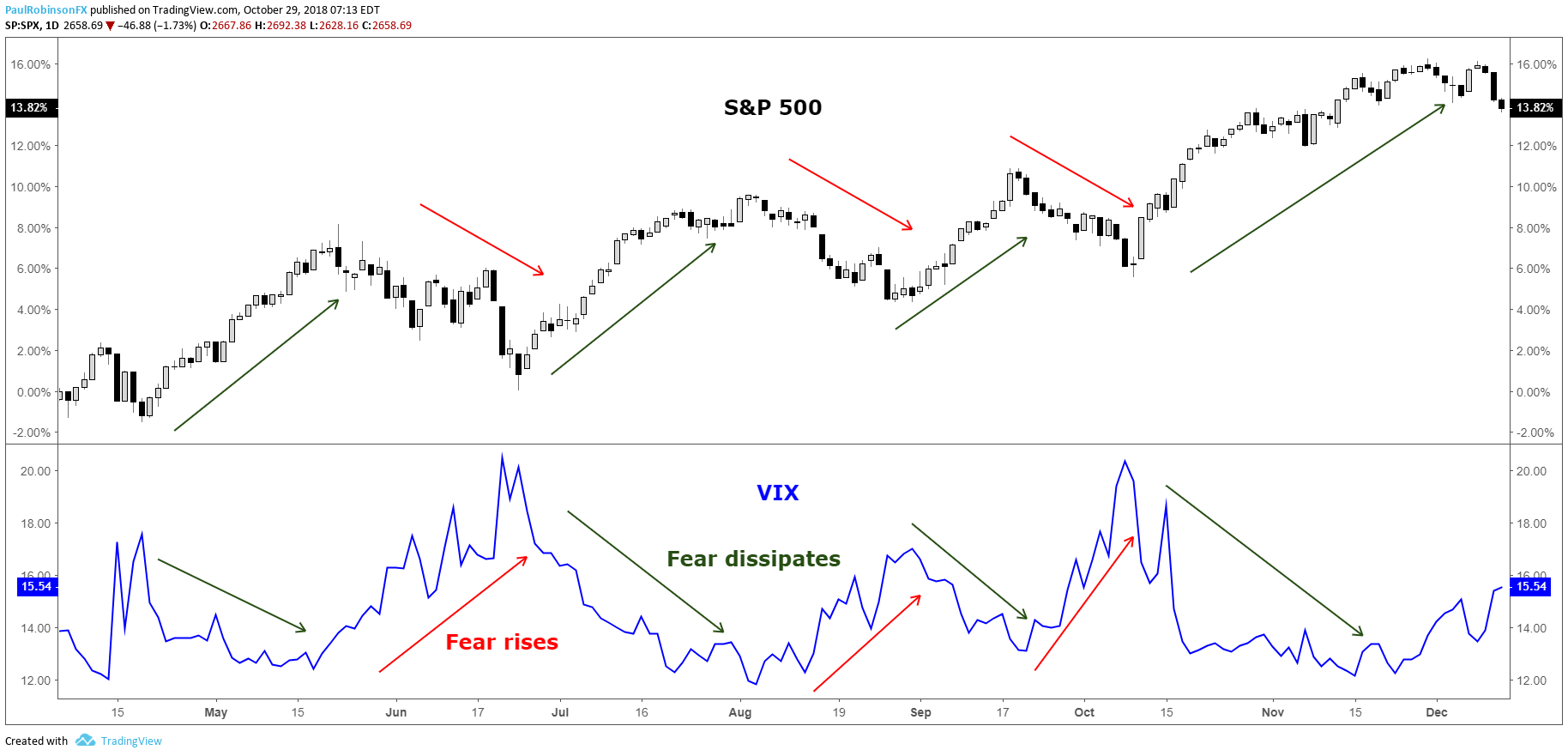
VIX指数は今後30日間のS&P 500の予想変動範囲を表現していて、予想変動範囲(%) = ${\displaystyle {\mbox{VIX}}/{\sqrt {12}}}$ である。例えばVIX指数が18の場合は予想変動範囲が5.2%である。ただし現実にはS&P 500が下落する場合はVIXは上昇する傾向があり、VIXとS&P 500のパフォーマンスは負の相関関係にある。その統計的傾向から俗に恐怖指数（きょうふしすう、英: fear index）とも呼ばれる。

2003年の改訂

2003年よりCBOEはゴールドマンサックスと共同して開発したより精度の高い計算方法でのVIX指数を公表するようになっている。

1993年当初のVIX指数はS&P 100に基づくものであったが、2003年9月22日よりS&P 500に基づく物に変更し、計算方法も修正し、元々のVIX指数をCBOE S&P 100ボラティリティ指数（VXO指数）に改名した。2003年9月22日より前のVIX指数はVXO指数の事を指している場合がある。

理論的バックグラウンド

理論的にはVIX指数は満期までのS&P 500のボラティリティの平均値の期待値として解釈される。満期を ${\displaystyle T}$ としたVIX指数は以下の式で算出される。

${\displaystyle VIX_{T}=100\times \sigma ,}$

${\displaystyle \sigma ^{2}={\frac {2}{T}}\sum _{i}e^{RT}{\frac {Q(K_{i})}{K_{i}^{2}}}\Delta K_{i}-{\frac {1}{T}}\left[{\frac {F-K_{0}}{K_{0}}}\right]^{2}}$

ここで ${\displaystyle R}$ は金利であり、${\displaystyle F}$ は満期を ${\displaystyle T}$ とするオプションのインデックス価格に対して望ましいレベルの先渡価格のインデックスである。${\displaystyle K_{i}}$ はオプションの行使価格の水準を表しており、行使価格の小さい方から昇順で番号付けられていて、${\displaystyle K_{0}}$ が ${\displaystyle F}$ を下回る最も大きな行使価格の値となるようになっている。${\displaystyle \Delta K_{i}}$ は ${\displaystyle K_{i 1}}$ と ${\displaystyle K_{i-1}}$ の差分の2分の1 ${\displaystyle (K_{i 1}-K_{i-1})/2}$ である。${\displaystyle Q(K_{i})}$ は行使価格 ${\displaystyle K_{i}}$、満期 ${\displaystyle T}$ のオプション価格のビットアスクスプレッドの中点となる。ただし、${\displaystyle K_{i}$ ならばプットオプション、${\displaystyle K_{i}>K_{0}}$ ならばコールオプションの価格が用いられている。

第2項は補正としての意味合いが強く、VIX指数の理論的なバックグラウンドを理解する上で重要なのは第1項の総和である。そこで第2項は無視して、第1項について考えてみる。第1項は積分を離散化したもので、あらゆる水準の行使価格でのオプションが市場で取引可能であるとすれば、次の積分形式での表示が可能である。

${\displaystyle \sigma ^{2}={\frac {2}{T}}\left(\int _{0}^{F}e^{RT}{\frac {P(K,T)}{K^{2}}}dK \int _{F}^{\infty }e^{RT}{\frac {C(K,T)}{K^{2}}}dK\right)}$

ここで ${\displaystyle C(K,T),P(K,T)}$ はそれぞれ満期 ${\displaystyle T}$、行使価格 ${\displaystyle K}$ のコールオプションとプットオプションの価格を指す。この時、リスク中立確率測度による期待値を ${\displaystyle E^{*}}$ で表すと、リスク中立確率測度の定義から

${\displaystyle C(K,T)=E^{*}[e^{-RT}\max\{S(T)-K,0\}],\quad P(K,T)=E^{*}[e^{-RT}\max\{K-S(T),0\}]}$

となる。ここで ${\displaystyle S(T)}$ は満期 ${\displaystyle T}$ におけるオプションの原資産の価格である。よって

${\displaystyle \sigma ^{2}={\frac {2}{T}}E^{*}\left[\int _{0}^{F}{\frac {\max\{K-S(T),0\}}{K^{2}}}dK \int _{F}^{\infty }{\frac {\max\{S(T)-K,0\}}{K^{2}}}dK\right]}$

と表されることが分かる。ここでCarr-Madan の展開公式から次の式変形が可能である。

${\displaystyle \int _{0}^{F}{\frac {\max\{K-S(T),0\}}{K^{2}}}dK \int _{F}^{\infty }{\frac {\max\{S(T)-K,0\}}{K^{2}}}dK=-\log S(T) \log F {\frac {S(T)-F}{F}}}$

したがって

${\displaystyle \sigma ^{2}={\frac {2}{T}}\left(-E^{*}[\log S(T)] \log F {\frac {E^{*}[S(T)]-F}{F}}\right)}$

となる。現時点を ${\displaystyle 0}$ 時点とすると先渡価格の無裁定価格は ${\displaystyle F=E^{*}[S(T)]=e^{RT}S(0)}$ なので次が得られる。

${\displaystyle \sigma ^{2}={\frac {2}{T}}{\Big (}RT-E^{*}[\log S(T)-\log S(0)]{\Big )}}$

ここで原資産価格 ${\displaystyle S}$ のリスク中立確率測度下での価格変動がボラティリティが変動する幾何ブラウン運動に従うとする。つまり

${\displaystyle S(T)=S(0) \int _{0}^{T}RS(t)dt \int _{0}^{T}v(t)S(t)dW^{*}(t)}$

であるとする。ただし ${\displaystyle W^{*}}$ はリスク中立確率測度下でのブラウン運動で、${\displaystyle v}$ は時間によって変動するボラティリティである。この時、伊藤の公式から

${\displaystyle \log S(T)=\log S(0) \int _{0}^{T}\left(R-{\frac {v^{2}(t)}{2}}\right)dt \int _{0}^{T}v(t)dW^{*}(t)=\log S(0) RT-{\frac {1}{2}}\int _{0}^{T}v^{2}(t)dt \int _{0}^{T}v(t)dW^{*}(t)}$

となる。これを ${\displaystyle \sigma ^{2}}$ に代入し、整理すれば

${\displaystyle \sigma ^{2}=E^{*}\left[{\frac {1}{T}}\int _{0}^{T}v^{2}(t)dt\right]-{\frac {2}{T}}E^{*}\left[\int _{0}^{T}v(t)dW^{*}(t)\right]}$

が得られる。第2項は確率積分の期待値なので ${\displaystyle v}$ に妥当な仮定を課せばその値は0である。つまり次の結果が得られる。

${\displaystyle \sigma ^{2}=E^{*}\left[{\frac {1}{T}}\int _{0}^{T}v^{2}(t)dt\right]}$

よって

${\displaystyle VIX_{T}=100\times {\sqrt {E^{*}\left[{\frac {1}{T}}\int _{0}^{T}v^{2}(t)dt\right]}}}$

となる。したがってVIX指数は満期までの平均ボラティリティにリスク中立確率測度で期待値を取ったものを基準化した指数である。CBOEが発表しているVIX指数はS&P 500を原資産としたオプション価格と先渡価格から計算されるので、VIX指数はS&P 500のボラティリティに対するものとなる。またCBOEが発表しているVIX指数の満期は30日である。

VIX指数の金融派生商品

VIX指数を原資産とした金融派生商品であるVIX先物（VX）やVIXオプションも取引されている。VIX指数のボラティリティ指数（ボラティリティのボラティリティ）であるVVIX指数もCBOEは公表している。
日本国内の証券取引所においては、VIX先物指数に連動するETFやETNが上場していたが、2024年現在は全て上場廃止となっている。
VIX先物取引については、楽天証券、GMOクリック証券、IG証券が、CFD取引の銘柄という形で取り扱っている。いずれの証券会社においても、買建て、売建て両方とも可能であるが、市場の変動状況によっては新規の売建てが制限される場合がある。

バリアンススワップとバリアンスリスクプレミアム

将来の株価の対数収益率の分散に対する先渡契約をバリアンススワップ (英: variance swap) と言う。またバリアンススワップにおける先渡価格をバリアンススワップレートと言い、S&P 500に対する満期が30日のバリアンススワップレートはその値が理論上はVIXと同じであるため、近似値としてVIXが使用されることがある。

また実現した株価の対数収益率の分散の平均値（実現ボラティリティ）よりVIXの方が高くなることが統計的に確かめられている。このVIXと実現ボラティリティの差をバリアンスリスクプレミアム (英: variance risk premium) と呼ぶ。

批判

ヒストリカル・ボラティリティとの差

VIX指数はインプライド・ボラティリティを用いているが、インプライド・ボラティリティがオプションを利用した複雑な計算をしているにもかかわらず、過去の値動きから単純に標準偏差を計算しただけのヒストリカル・ボラティリティと結果が大差無いという批判がある。

不正操作

2017年5月23日に、VIX指数の計算に使われるS&P 500のオプションは取引の少ない物が含まれていて、それを使用することでVIX指数を操作することが可能であるうえ、その対象となっているS&P 500のオプションだけ不自然に取引が多いという論文が発表された。更に、2018年2月12日に実際にVIX指数を不正操作している人がいるという匿名の告発が証券取引委員会になされた。

過去の主要な高値・低値

高値

• 1990年8月23日 イラク軍クウェート侵攻…36.47
• 1997年10月28日 アジア通貨危機…48.64
• 1998年10月8日　 ロシアデフォルト（LTCM破綻）…49.53
• 2001年9月21日 アメリカ同時多発テロ…49.35
• 2002年7月24日　エンロン不正会計事件…48.46
• 2002年8月5日　 ワールドコム破綻…45.21
• 2003年3月12日 イラク戦争勃発…34.40
• 2008年9月18日 リーマン・ブラザーズ破綻…42.16
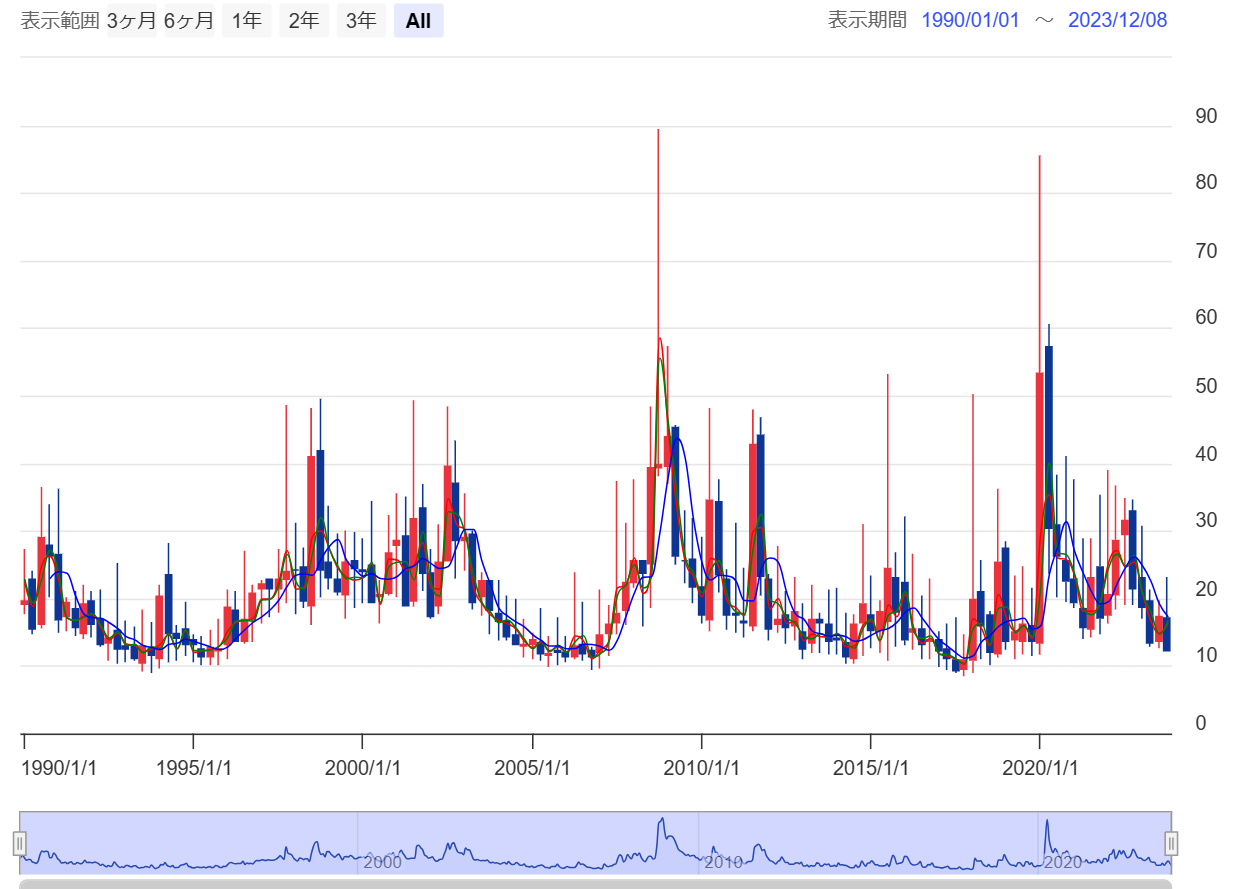
• 2008年10月24日 世界金融危機…89.53（1993年以降の最高値）
• 2010年5月21日　ギリシャを筆頭とするPIIGSの国債懸念…48.20
• 2011年8月9日　S&Pが米国債を格下げ…47.56
• 2011年10月4日　ギリシャ国債のデフォルト危機…46.88
• 2015年8月24日　中国経済失速懸念…53.29
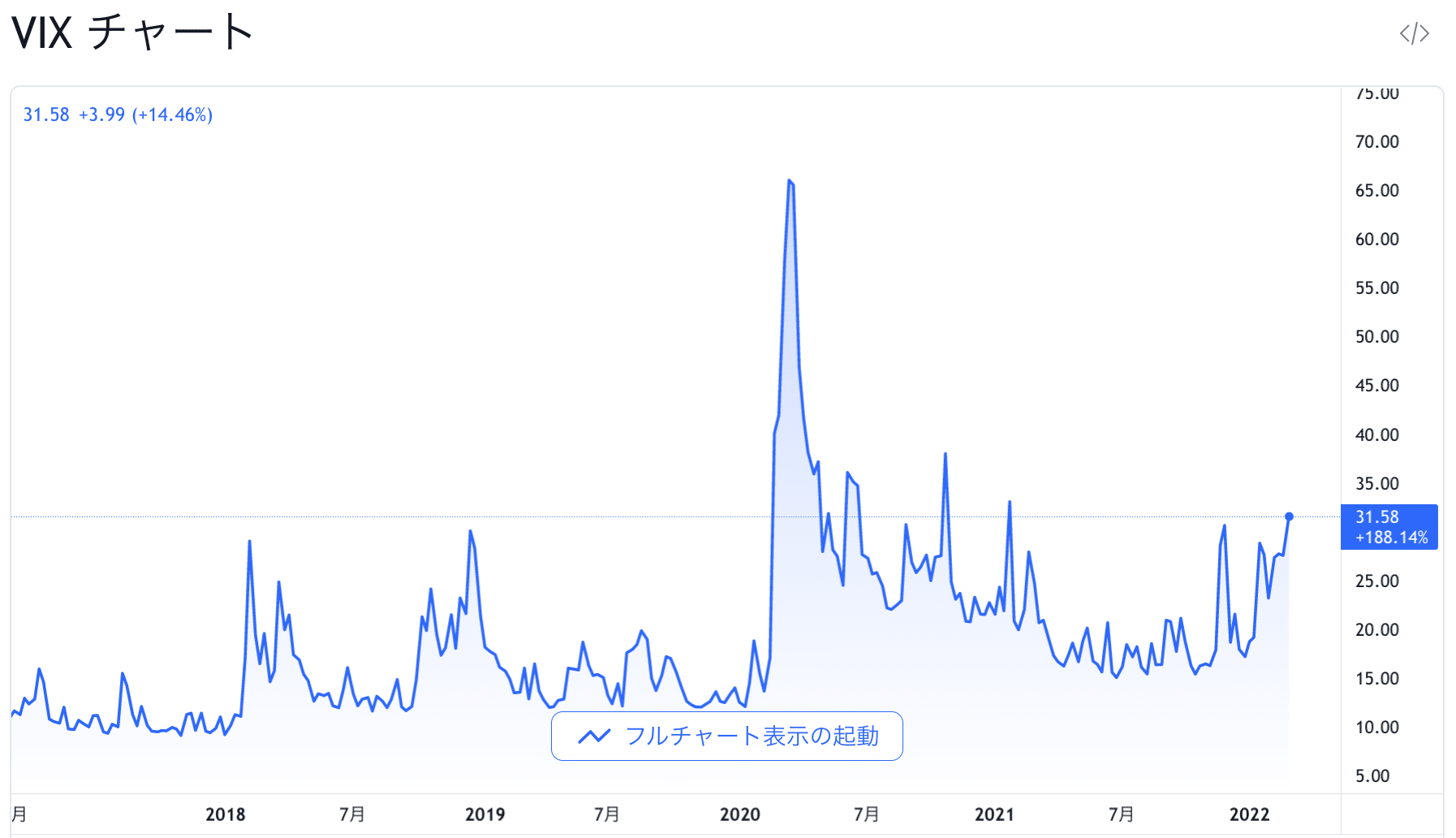
• 2018年2月6日　米雇用統計での賃金上昇をきっかけとした長期金利上昇、VIXショック「変動幅は過去最大規模」…50.30
• 2020年3月18日　新型コロナウイルスによるパンデミック …85.47
• 2024年8月5日　米雇用統計での失業率等悪化をきっかけとした世界同時株安 …65.73

低値

• 1993年12月27日… 8.89
• 2006年11月22日 …9.81
• 2007年1月24日 … 9.87
• 2017年7月26日 …8.84
• 2017年11月3日 …8.99
• 2017年11月24日 …8.56（1993年以降の最低値）
• 2018年1月4日 …8.92

脚注

出典

外部リンク

• Vix Index - Cboe
• ^VIX Interactive Stock Chart | CBOE Volatility Index Stock - Yahoo Finance